OC11_G50.5 Orden y Caos: #2 La sucesión de Fibonacci

La sucesión de Fibonacci fue propuesta por Leonardo de Pisa Fibonacci, él se basó en la sucesión reproductiva de los conejos por ejemplo en la fig. 1 se muestra esta sucesión.

Fig. 1

Esta sucesión describe una serie de números, que se obtiene por adición de los dos números anteriores, obteniéndose la serie: 0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.

¿Qué situaciones describe esta serie? Bien, esta serie se hizo especialmente famosa por describir las proporciones de la naturaleza de forma muy amplia además se ha extendido en campos como las matemáticas, ciencias de la computación, biología o teoría de juegos.

Las famosas proporciones que describen la serie de Fibonacci se van obteniendo mediante cocientes entre números de la serie, por ejemplo, si se divide dos números consecutivos de la serie obtendrás una proporción de 0.618, por ejemplo, 21 entre 34. Si divides dos números alternos obtendrás 0.382, por ejemplo 55 entre 144. Todas estas proporciones son las llamadas "proporciones áureas"

Las sucesiones de Fibonacci también representan un rol dentro de la naturaleza por ejemplo:

En la Botánica:

La serie se puede encontrar en ciertas flores que tienen un número de pétalos que suelen ser términos de dicha sucesión; de esta manera el lirio tiene 3 pétalos, algunos ranúnculos 5 o bien 8, las margaritas y girasoles suelen contar con 13, 21, 34, 55 o bien 89.

En la Genética:

El número de descendientes en cada generación de una abeja macho o zángano nos conduce a la sucesión de Fibonacci, y por lo tanto, al número áureo.

Una vez inseminada la abeja reina por un zángano (de otro enjambre), aquella se queda en su colmena y ya no sale más, dedicándose a la puesta de huevos que ella misma va fecundando o no, dando origen así a abejas obreras, o bien reinas, en el primer caso y machos o zánganos en el segundo. Si observamos el árbol genealógico de un zángano, podemos ver como el número de abejas en cada generación es uno de los términos de la sucesión de Fibonacci.

Formula explícita:

Demostración:

f_n+2- f_n+1- f_n=0, con f₀=0 y f₁=1

EC: t² - t -1 = 0

Soluciones:

$t=\frac{1\pm\sqrt 5}{2}$

De esta forma la fórmula explícita de la sucesión de Fibonacci es:

$f_n=b\left(\frac{1+\sqrt5}2\right)^n+d\left(\frac{1-\sqrt5}2\right)^n$

Se toman las condiciones iniciales para satisfacer el sistema de ecuaciones:

$\left.\begin{array}{rcl}b+d & = & 0 \\ b\left(\frac{1+\sqrt5}2\right)+d\left(\frac{1-\sqrt5}2\right)&=&1\end{array}\right\}$

Las soluciones serían:

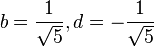
$b=\frac1{\sqrt5},d=-\frac1{\sqrt5}$

Por lo tanto cada uno de los números de Fibonacci puede ser expresado de la siguiente manera:

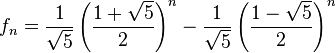
$f_n=\frac1{\sqrt5}\left(\frac{1+\sqrt5}2\right)^n-\frac1{\sqrt5}\left(\frac{1-\sqrt5}2\right)^n$

Para simplificar la expresión se puede tomar el número áureo:

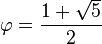
$\varphi=\frac{1+\sqrt5}2$

Entonces la expresión se reduce a:

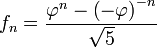$f_n=\frac{\varphi^n-\left(-\varphi\right)^{-n}}{\sqrt5}$ (Fin de la demostración)

Para todas aquellas personas que quieran ampliar sobre el tema les recomendamos este link aborda varios temas interesantes sobre la sucesión de Fibonacci y el número áureo: http://www.bloganavazquez.com/tag/serie-de-fibonacci/

http://www.youtube.com/watch?v=fuCPXzAhNM4&feature=related

OC11_G50.5 Orden y Caos

Bienvenidos

Archivo del blog

jueves, 2 de junio de 2011

#2 La sucesión de Fibonacci

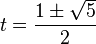
No hay comentarios:

Publicar un comentario